Statyczne drzewa binarne
Na początku kursu algorytmiki prezentowaliśmy ideę wyszukiwania binarnego na przykładzie problemu szybkiego wyszukiwania zadanego elementu w uporządkowanej tablicy liczb. Jest to bardzo dobry sposób, o ile rozpatrywany zbiór elementów nie ulega zmianie. Bardzo silnie polegamy bowiem na uporządkowaniu elementów tablicy, gdybyśmy więc chcemy z niej usuwać lub dodawać liczby, musimy potencjalnie wykonać o wiele więcej operacji – przy usuwaniu elementu ze środka tablicy trzeba "załatać" dziurę, przesuwając wszystkie dalsze elementy. Podobnie, trzeba przesunąć wszystkie elementy od miejsca, w którym chcemy wstawić nową liczbę.
Niestety, na zwykłej, "płaskiej" tablicy trudno osiągnąć lepszą złożoność operacji wstawienia lub usunięcia elementu. Załóżmy zatem, że mamy do przechowania zbiór elementów (liczb), który będzie się zmieniał, podczas gdy my będziemy musieli szybko wyszukiwać konkretne elementy w zbiorze (czyli odpowiadać na pytania "czy jest tam zadana liczba", a czasem "ile jest w zbiorze liczb mniejszych od zadanej"). Spróbujmy teraz pomyśleć o naszych przechowywanych elementach nieco inaczej niż dotychczas.
Po pierwsze, komórki pamięci zorganizujemy w tak zwane drzewo binarne – pierwsza komórka będzie "ojcem" dwóch kolejnych komórek, każda z nich z kolei będzie miała dwoje "dzieci" w postaci kolejnych komórek, i tak dalej, jak na poniższym rysunku:
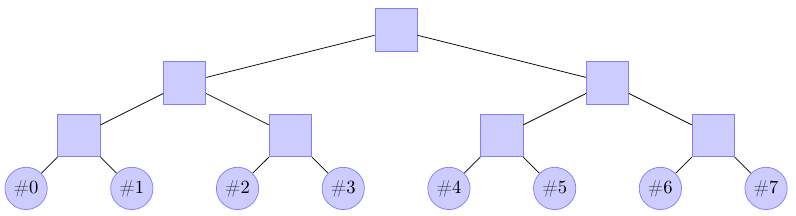
Za chwilę wyjaśni się, jak opisać takie drzewo w języku zrozumiałym dla komputera. Na razie wprowadźmy potrzebne pojęcia: komórki w drzewie nazywane są węzłami. Komórki na samym dole (nie posiadające już potomków) to liście drzewa, a pozostałe węzły to węzły wewnętrzne.
W drzewie moglibyśmy przechowywać oryginalne elementy (które wcześniej trzymaliśmy w tablicy) – wykorzystamy to pod koniec lekcji. Na razie, zamiast tego, liście drzewa będą przechowywały liczniki poszczególnych elementów naszego zbioru – informację o tym, ile jest w zbiorze zer, jedynek, dwójek, trójek itd. Natomiast węzły wewnętrzne przechowywać będą sumę elementów z dwóch węzłów potomnych. Na rysunku powyżej liście oznaczono okręgami z liczbą oznaczającą element, którego liczbę wystąpień przechowujemy w tym miejscu. Węzły wewnętrzne oznaczone są kwadratami.
Czyli jeśli przykładowo mamy w zbiorze 10 elementów \(3\), to w kółku oznaczonym \(\#3\) będziemy trzymać wartość 10. Jeśli oprócz dziesięciu trójek będziemy mieli jeszcze pięć dwójek, to kwadratowe pole powyżej liści \(\#2\) i \(\#3\) będzie przechowywać wartość \(5 + 10 = 15\). W korzeniu drzewa znajdzie się w takim razie liczba wszystkich elementów zbioru. Taka sytuacja została pokazana na rysunku poniżej. Wpisane zostały także przykładowe wartości w pozostałe liście, a węzły wewnętrzne zawierają stosowne sumy liczb przechowywanych w lewym i prawym potomku.
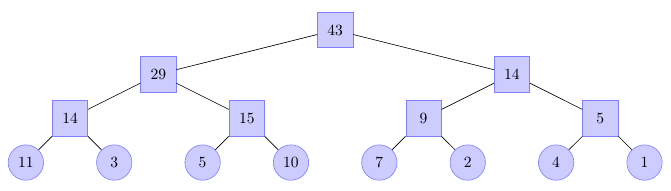
Przyjmijmy na razie założenie, które uprości kwestie techniczne w dalszej części lekcji: liczby, na których operujemy, pochodzą z zakresu \([0, 2^k -1]\), gdzie \(k\) jest sensownie małe. Powód takiego ograniczenia jest bardzo przyziemny – na drzewo będziemy potrzebowali dużo pamięci: proporcjonalnie do rozmiaru tego przedziału. W zdecydowanej większości zadań algorytmicznych, w których rozwiązanie wzorcowe korzysta z podobnego drzewa, wartość \(k\) nie przekracza \(20\), co daje zakres \([0, 1\;048\;575]\) (trochę więcej niż milion różnych elementów).
Zastanowimy się teraz jak rzeczywiście zmieniać zawartość naszego zbioru elementów i jak przechowywać całe drzewo w programie. Nieco przewrotnie okazuje się, że najprościej reprezentować drzewo za pomocą jednowymiarowej tablicy. Spójrzmy raz jeszcze na wcześniejszy rysunek, jednak ze zmienioną numeracją węzłów drzewa:
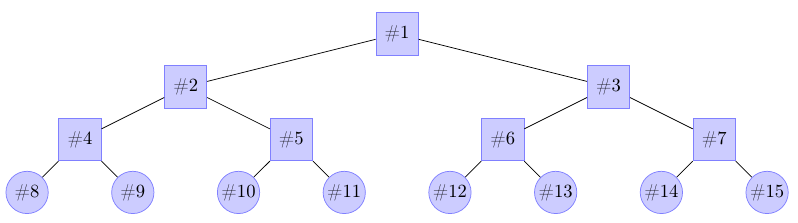
W takim ustawieniu węzeł o numerze \(\#i\) ma rodzica o numerze \(\#i/2\) (o ile nie jest korzeniem), lewego potomka o numerze \(\#2i\) i prawego o numerze \(\#2i + 1\) (o ile nie jest liściem). Korzeniowi nadajemy numer \(\#1\), łączny rozmiar drzewa jest równy dwukrotności liczby liści (minus nieużywany element \(\#0\)). Numer pierwszego liścia jest taki, jak liczba liści. Definicja drzewa w programie mogłaby zatem wyglądać następująco:
const int LEAF_COUNT = 1024; //liczba liści, w tym przykładzie 2^10
const int TREE_SIZE = 2 * LEAF_COUNT; //rozmiar całego drzewa
int tree[TREE_SIZE];
Sprawdzanie czy element \(x\) znajduje się w zbiorze
Dla dowolnego \(x\) licznik wystąpień tego elementu w zbiorze znajduje się w
tree[x + LEAF_COUNT], więc sprawdzenie wystąpienia jest natychmiastowe
i nie trzeba pisać wyszukiwania binarnego. Nasze drzewo w tym miejscu niczym
się nie różni od tablicy, która w poszczególnych indeksach zlicza wystąpienia
różnych liczb.
Istotnym problemem jest oczywiście kwestia przechowywania dużych liczb w takim drzewie (założyliśmy, że dane pochodzą z małego zakresu), ale do tego jeszcze wrócimy.
Dodawanie i usuwanie elementów
Jeśli chcemy dodać element \(x\), to musimy zwiększyć o 1 wartość licznika
w liściu odpowiadającym tej wartości (czyli w węźle LEAF_COUNT + x)
oraz wszystkich węzłów wewnętrznych na drodze od tego liścia do korzenia.
Analogicznie możemy usuwać elementy – zmniejszając licznik w liściu i
całej ścieżce do korzenia – albo w jednej operacji wstawić/usunąć wiele
elementów o wartości \(x\). Poniższa funkcja jest napisana w sposób uniwersalny,
tzn. potrafi ona zarówno dodać \(d\) elementów o wartości \(x\) (dla dodatnich wartości argumentu
d) jak i usuwać elemeny (dla ujemnych wartości argumentu d).
void modify(int x, int d)
{
int current = x + LEAF_COUNT; //zaczynamy w liściu odpowiadającym wartości 'x'
//idziemy w górę drzewa
while (current > 0) {
tree[current] += d;
current /= 2;
}
}
Czas działania tej operacji jest proporcjonalny do liczby poziomów drzewa – zaczamy pętlę w liściu, kończymy po osiągnięciu korzenia, z każdym obrotem pętli przechodzimy na jeden poziom wyżej. Ponieważ na każdym poziomie liczba węzłów maleje dwukrotnie, to złożoność operacji jest \(O(\log n)\), gdzie przez \(n\) rozumiemy rozmiar drzewa. Jest to istotnie lepsze od czasu \(O(n)\), który mielibyśmy w przypadku użycia tablicy posortowanych liczb!
Inne operacje
Na razie potrafimy zmieniać liczność elementów określonej wartości oraz pytać o ich wystąpienia w drzewie. Jakie jeszcze informacje możemy wyciągać w efektywny sposób?
Znajdowanie najmniejszego (największego) elementu
Bez straty ogólności skupimy się na metodzie znajdowania elementu najmniejszego.
Szukanie maksimum przebiega analogicznie. Zakładamy też, że w drzewie znajduje
się przynajmniej jeden element – licznik elementów w korzeniu drzewa
(tree[1]) musi być większy od zera.
Ponieważ mniejsze elementy są przechowywane w liściach bardziej "na lewo", to chcemy tak naprawdę znaleźć pierwszy od lewej liść, którego licznik jest większy od zera. Oczywiście nie przeglądamy po kolei liści, ponieważ w pesymistycznym przypadku element minimalny znajdzie się w ostatnim liściu drzewa, a my wykonamy \(O(n)\) operacji zanim się o tym przekonamy.
Zamiast tego zaczniemy szukanie minimum od korzenia, a dokładniej od sprawdzenia jego potomków po lewej i prawej stronie. Jeśli lewy potomek korzenia ma licznik elementów większy od zera, to możemy zupełnie zignorować prawego potomka, ponieważ każdy element po prawej stronie jest większy od dowolnego elementu po lewej stronie, więc zaglądanie tam jest nieopłacalne z perspektywy szukania minimum. Jeśli jednak lewy potomek ma wartość zero (nie ma żadnych elementów w lewej połowie drzewa), to niestety musimy skupić się na prawej połowie.
W obu przypadkach schodzimy o jeden poziom w dół drzewa i odcinamy z rozważań połowę liści. Powtarzamy wcześniejsze rozumowanie traktując miejsce, w którym się znaleźliśmy jako zupełnie niezależne drzewo – zapominamy, że był jakiś korzeń i druga połowa drzewa. Tu i teraz mamy nowe, mniejsze drzewo o nowym korzeniu i działamy dokładnie tak samo. Z każdym takim krokiem znowu obniżamy się o jeden poziom i redukujemy liczbę liści o połowę, aż w końcu będziemy mieli drzewo jednoelementowe, czyli poszukiwany w oryginalnym drzewie minimalny, niepusty liść.
int find_min()
{
int current = 1; //zaczynamy w korzeniu
//kończymy gdy znajdziemy się w liściu
while (current < LEAF_COUNT) {
int left = 2 * current;
int right = 2 * current + 1;
if (tree[left] > 0)
current = left;
else
current = right;
}
//zwracamy numer liścia, a nie indeks w tablicy reprezentującej drzewo
return current - LEAF_COUNT;
}
Liczenie elementów mniejszych od \(x\)
W graficznym przedstawieniu problemu chodzi nam o posumowanie wartości we
wszystkich liściach na lewo od LEAF_COUNT + x. Oczywiście chcemy (i
możemy) zrobić to sprytniej niż rzeczywiście przechodzić po wszystkich liściach.
Skorzystamy tutaj z sum elementów przetrzymywanych w węzłach wewnętrznych drzewa. Zaczniemy w liściu i będziemy kierować się w stronę korzenia. Ilekroć wchodząc na poziom wyżej wejdziemy "od prawej strony", musimy dodać do wyniku wszystkie elementy zapamiętane w lewej połowie poddrzewa. Na przykład, jeśli chcemy policzyć ile jest elementów mniejszych od \(3\), to dla drzewa pokazanego na rysunku powyżej:
- Zaczynamy w liściu odpowiadającym wartości \(3\), czyli w \(\#11\).
- Idziemy w górę do węzła \(\#5\). Ponieważ weszliśmy z prawej strony, to do wyniku dodajemy zawartość lewego potomka węzła \(\#5\), czyli liczbę zapamiętaną w \(\#10\).
- Idziemy w górę do \(\#2\). Ponownie wchodzimy z prawej strony, więc do wyniku dodajemy liczbę z węzła \(\#4\).
- Ostatni raz idziemy w górę i przechodzimy do korzenia. Nie dodajemy niczego do wyniku, ponieważ weszliśmy z lewej strony. Jesteśmy w korzeniu, więc kończymy.
Warto zauważyć, że jeśli węzeł jest prawym potomkiem swojego rodzica w drzewie, to jego numer jest liczbą nieparzystą, a jego "lewy" sąsiad ma numer o jeden mniejszy. Korzystamy z tego w poniższej funkcji.
int less_than(int x)
{
int current = x + LEAF_COUNT;
int result = 0;
while (current != 1) {
//sprawdzamy parzystość bieżącego węzła
if (current % 2 == 1)
result += tree[current - 1];
current /= 2;
}
return result;
}
Jeśli potrzebujemy podobnych operacji (znaleźć elementy mniejsze-równe, większe, większe-równe lub należące do zadanego przedziału), to zamiast pisać dalsze fragmenty kodu bardzo podobne do powyższego, lepiej pójść na skróty:
- Elementy mniejsze-równe \(x\) otrzymamy wyszukując liczbę elementów
mniejszych od \(x + 1\): wywołanie
less_than(x + 1);. - Większe od \(x\) mamy poprzez znalezienie liczby mniejszych-równych \(x\) i
odjęcie znalezionej wartości od liczby wszystkich elementów:
tree[1] - less_than(x + 1);. - Podobnie dla większych-równych \(x\):
tree[1] - less_than(x); - Dla przedziału \([a, b]\) szukamy liczb mniejszych-równych \(b\) i od
znalezionej wartości odejmujemy liczbę elementów mniejszych od \(a\):
less_than(b + 1) - less_than(a);
Co z dużymi liczbami?
Wcześniej założyliśmy, że elementy, na których operujemy, są liczbami z relatywnie niewielkiego zakresu. Wynikało to ze sposobu działania liści w naszym drzewie: każdy z nich trzymał nie pojedynczy element, a licznik elementów określonej wartości. Takie drzewa w literaturze zwykle nazywane są drzewami licznikowymi.
W rzeczywistości nie zawsze jest tak wygodnie, często trzeba sobie radzić z liczbami dowolnego rozmiaru. Prezentowana wyżej struktura danych ma rozmiar ustalony na sztywno w czasie kompilacji (dlatego mówimy, że jest statyczna) i raczej nie możemy przydzielić sobie tablicy rozmiaru kilku miliardów elementów.
Czasami można obejść problem liczb z dużego zakresu, o ile różnych wartości może być niewiele. Wtedy wczytujemy oryginalne dane i przed podjęciem jakichkolwiek działań, przenumerowujemy wartości z dużego zakresu na sztuczne wartości z wygodnego dla nas małego zakresu. Na przykład dane wejściowe operujące na liczbach \(10\), \(456\) i \(1234\) równie dobrze mogłyby działać na liczbach (odpowiednio) \(0\), \(1\) i \(2\).
Niestety nie zawsze możemy pozwolić sobie na luksus pamięciowy związany z wczytaniem wszystkich danych wejściowych i jeszcze wygospodarowaniem dodatkowego miejsca na "księgowość" związaną z przeliczaniem oryginalnych wartości na sztuczne i odwrotnie.
W takich momentach należy zwrócić się w stronę struktur dynamicznych, w szczególności drzew wyszukiwań binarnych (ang. BST – Binary Search Trees). Nie opiszemy ich tutaj, a jedynie wspominamy dla pełności lekcji. Przejdziemy natomiast do opisu statycznych drzew binarnych działających w oparciu o konkretne elementy przechowywane w liściach, a nie, jak wcześniej, jedynie w oparciu o ich liczności. Będziemy zatem mogli przechowywać również duże liczby w drzewie.
Drzewa przedziałowe
Rozważmy teraz problem, który jest przedmiotem jednego z zadań dołączonych do lekcji. Mamy ciąg liczb \(a_1, a_2, \ldots, a_n\) oraz pewne przedziały zadane przez pary \([L, R]\). Chcemy dla każdego takiego przedziału poznać największy element spośród \(a_L, a_{L+1},\ldots, a_{R-1}, a_R\).
Możemy zmodyfikować trochę pomysł z wcześniejszej części tej lekcji. W węzłach drzewa zamiast sumy, będziemy pamiętali maksimum z wszystkich elementów poniżej. Dla ciągu liczb \(11, 3, 5, 10, 7, 2, 4, 1\) otrzymamy zatem:
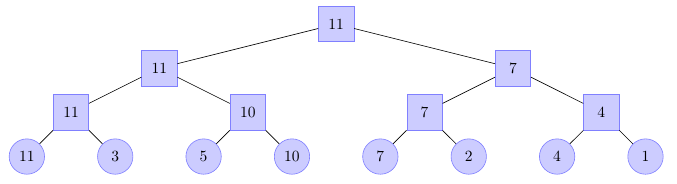
Drzewo takiego rodzaju nazywa się czasami w literaturze drzewem maksimowym albo turniejowym. W ogólności zarówno drzewo maksimów jak i drzewo licznikowe należy do szerszej klasy drzew, nazywanych przedziałowymi. Nazwa bierze się z częstego operowania na przedziałach elementów zamiast na pojedynczych elementach. Już w przypadku drzewa licznikowego określiliśmy jedną operację przedziałową: zliczanie elementów mniejszych od zadanego \(x\).
Gdy chcemy odpowiedzieć na zapytanie o maksimum na przedziale \([L, R]\), musimy znaleźć pewien zbiór cząstkowych przedziałów reprezentowanych przez węzły drzewa przedziałowego. Takie mniejsze przedziały nazywa się przedziałami bazowymi. Gdy mamy przedziały bazowe, możemy sięgnąć do drzewa i wziąć maksimum z wartości przechowywanych w węzłach odpowiadającym przedziałom bazowym, otrzymując w ten sposób wynik całego zapytania. Pomocniczy rysunek przedstawiający przełożenie węzłów drzewa na podprzedziały powinien ułatwić zrozumienie pomysłu:
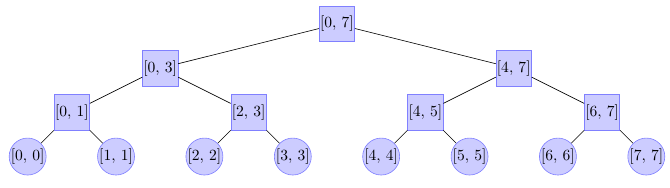
Dla przedziału wejściowego \([1, 7]\) zbiór przedziałów bazowych to \([1,1], [2, 3], [4, 7]\). Natomiast dla przedziału \([5, 6]\) zbiór przedziałów bazowych to \([5, 5], [6, 6]\). Do przedziałów bazowych wybieramy możliwie największe przedziały, dlatego w pierwszym przykładzie wybraliśmy \([4, 7]\), a nie np. \([4, 5]\) i \([6, 7]\).
Algorytm znajdowania przedziałów bazowych jest najbardziej skomplikowaną częścią drzew przedziałowych. Istnieje kilka sposobów wykonywania tej czynności, a prezentowana poniżej metoda jest jedynie propozycją.
- Dany jest przedział \([L, R]\). Zaczynamy w korzeniu drzewa, a odpowiadający mu przedział oznaczmy \([a, b]\).
- Jeśli \(P\) jest równy przedziałowi reprezentowanemu przez węzeł drzewa, w którym jesteśmy (czyli \(a = L\) i \(b = R\)), to tutaj znajduje się przedział bazowy i kończymy.
-
W przeciwnym przypadku mamy 3 możliwości:
-
\(P\) znajduje się w całości w lewym poddrzewie względem węzła, w którym się znajdujemy. Dzieje się tak wtedy, gdy \(R \leq \frac{a + b - 1}{2}\). Przechodzimy zatem do lewego potomka (który reprezentuje przedział \([a, \frac{a + b - 1}{2}]\) i kontynuujemy tamże szukania przedziałów bazowych dla \(P\).
- \(P\) znajduje się w całości w prawym poddrzewie, co ma miejsce, gdy \(L > \frac{a + b - 1}{2}\). Idziemy więc do prawego potomka, któremu odpowiada przedział \([\frac{a + b - 1}{2} + 1, b]\)
- Jeśli żaden z powyższych przypadków nie miał miejsca, wtedy \(P\) znajduje się częściowo zarówno po lewej jak i po prawej stronie. W takiej sytuacji "przecinamy" \(P\), dzieląc go na część znajdującą się w lewym poddrzewie \(P_L = [L, \frac{a + b - 1}{2}]\) i część znajdującą się w prawym poddrzewie \(P_R = [\frac{a + b - 1}{2} + 1, R]\).
void find_base(int v, int L, int R, int a, int b) //'v' jest numerem węzła w drzewie
{
if (L == a && R == b) {
//jesteśmy w przedziale bazowym
return;
}
int mid = (a + b - 1) / 2;
if (R <= mid) {
find_base(2 * v, L, R, a, mid);
} else if (L > mid) {
find_base(2 * v + 1, L, R, mid + 1, b);
} else {
find_base(2 * v, L, mid, a, mid);
find_base(2 * v + 1, mid + 1, R, mid + 1, b);
}
}
Pierwsze wywołanie find_base() zawsze powinno nastąpić w korzeniu
drzewa z właściwymi dla niego wartościami argumentów a i b.
Czyli dla naszego przykładowego drzewa o ośmiu liściach, wywołujemy:
find_base(1, L, R, 0, 7);
Napisanie operacji zmiany wartości elementu w liściu i idącą za tym potencjalną aktualizację maksimów na wyższych poziomach drzewa pozostawiamy jako ćwiczenie zawarte w jednym z zadań dołączonych do lekcji.
Co jeszcze w drzewie piszczy?
Drzewa przedziałowe są silnym i elastycznym narzędziem rozwiązywania wielu problemów algorytmicznych. Idea korzystania z nich jest bardzo podobna między zadaniami i prędzej czy później sprowadza się do działania na przedziałach bazowych. Główne różnice występują w danych, które chcemy trzymać w węzłach drzewa – mogą to być bardziej skomplikowane twory niż maksima z przedziałów, co pokazuje drugie z zadań dołączonych do tej lekcji.